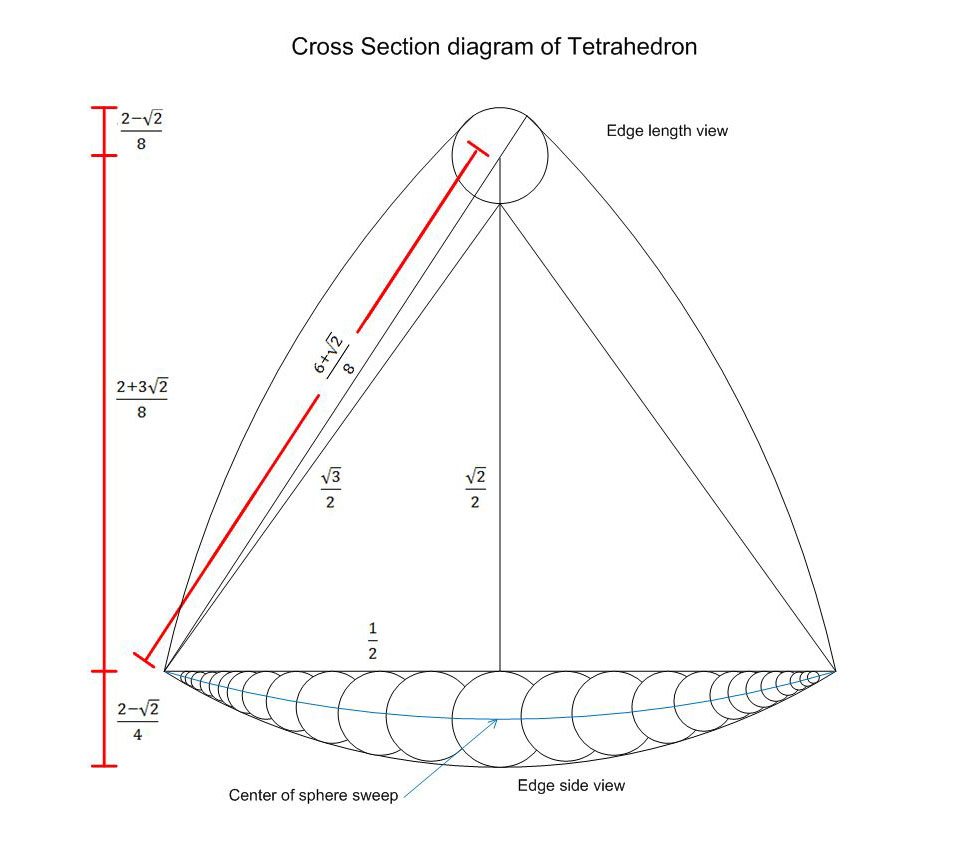
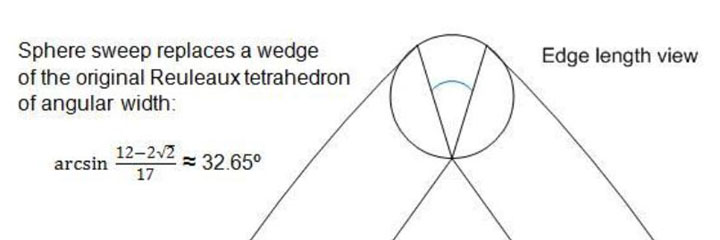
The Reuleaux tetrahedron can be modified into a 'solid of constant width' by replacing all six edges with sections of an 'envelope of spheres' - a sphere-sweep in ray tracing terminology. The resulting solid is spheroform and has tetrahedral symmetry.

The sphere envelopes extend between vertices on each edge of the unit tetradedron (edge length 1). The radius of each sphere in the envelope is given by the function:
Each sphere is tangent to the straight edge of an internal regular tetrhadron, and tangent to the surface of the Reuleaux tetrahedron.
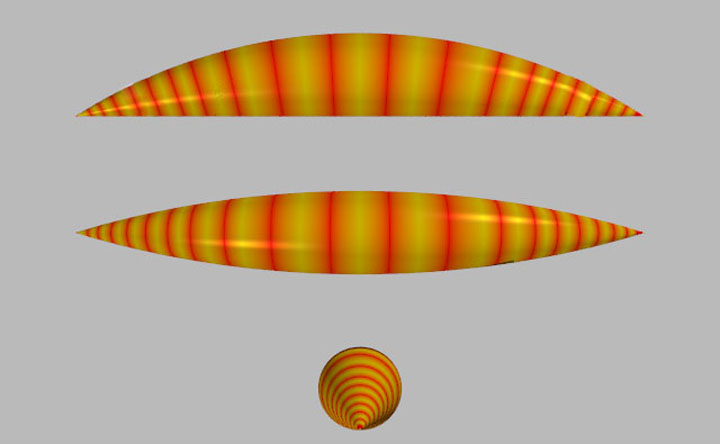
Rendered Sphere Sweep
Side view
Top view
Length view




Rendered Spheroform Tetrahedra